"Completing the Square" is where you ...
| ... take a Quadratic Equation like this: | and turn it into this: | |
ax2 + bx + c = 0
|
a(x+d)2 + e = 0
|
| For those of you in a hurry, I can tell you that: | |||
| and: |
But if you have time, let me show you how to "Complete the Square" yourself.
Completing the Square
Say we have a simple expression like x2 + bx. Having x twice in the same expression can make life hard. What can we do?
Well, with a little inspiration from Geometry we can convert it, like this:
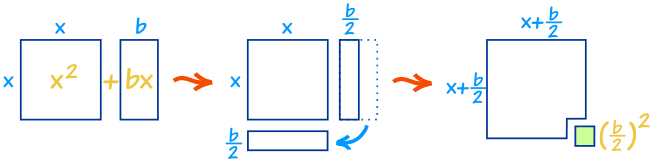
As you can see x2 + bx can be rearranged nearly into a square ...
... and we can complete the square with (b/2)2
In Algebra it looks like this:
| x2 + bx | + (b/2)2 | = | (x+b/2)2 | |
| "Complete the Square" |
So, by adding (b/2)2 we can complete the square.
And (x+b/2)2 has x only once, which is easier to use.
Keeping the Balance
Now ... you can't just add (b/2)2 without also subtracting it too! Otherwise the whole value would change.
So I will show you how to do it properly with an example:
| Start with: | ||
| ("b" is 6 in this case) | ||
Complete the Square:
| 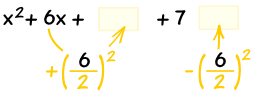
Also subtract the new term
| |
Simplify it and we are done.
| ||
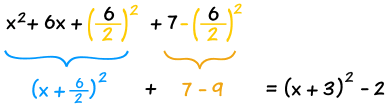 | ||
The result:
x2 + 6x + 7 = (x+3)2 - 2
And now x only appears once, and your job is done!
Now, let us look at a useful application: solving Quadratic Equations ...
Solving General Quadratic Equations by Completing the Square
We can complete the square to solve a Quadratic Equation (find where it is equal to zero).
But a general Quadratic Equation can have a coefficient of a in front of x2:
ax2 + bx + c = 0
But that is easy to deal with ... just divide the whole equation by "a" first, then carry on:
x2 + (b/a)x + c/a = 0
Steps
Now we can solve a Quadratic Equation in 5 steps:
- Step 1 Divide all terms by a (the coefficient of x2).
- Step 2 Move the number term (c/a) to the right side of the equation.
- Step 3 Complete the square on the left side of the equation and balance this by adding the same value to the right side of the equation.
We now have something that looks like (x + p)2 = q, which can be solved rather easily:
- Step 4 Take the square root on both sides of the equation.
- Step 5 Subtract the number that remains on the left side of the equation to find x.
Examples
I have two examples to show you how:
Example 1: Solve x2 + 4x + 1 = 0
Step 1 can be skipped in this example since the coefficient of x2 is 1
Step 2 Move the number term to the right side of the equation:
x2 + 4x = -1
Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation.
(b/2)2 = (4/2)2 = 22 = 4
x2 + 4x + 4 = -1 + 4
(x + 2)2 = 3
Step 4 Take the square root on both sides of the equation:
x + 2 = ±√3 = ±1.73 (to 2 decimals)
Step 5 Subtract 2 from both sides:
x = ±1.73 – 2 = -3.73 or -0.27
And here is an interesting and useful thing.
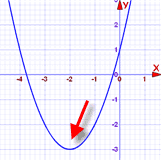
At the end of step 3 we had the equation:
(x + 2)2 = 3
It gives you the vertex (turning point) of x2 + 4x + 1: (-2, -3)
|  |
Example 2: Solve 5x2 – 4x – 2 = 0
Step 1 Divide all terms by 5
x2 – 0.8x – 0.4 = 0
Step 2 Move the number term to the right side of the equation:
x2 – 0.8x = 0.4
Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation:
(b/2)2 = (0.8/2)2 = 0.42 = 0.16
x2 – 0.8x + 0.16 = 0.4 + 0.16
(x – 0.4)2 = 0.56
Step 4 Take the square root on both sides of the equation:
x – 0.4 = ±√0.56 = ±0.748 (to 3 decimals)
Step 5 Subtract (-0.4) from both sides (in other words, add 0.4):
x = ±0.748 + 0.4 = -0.348 or 1.148
Why "Complete the Square"?
Why would you want to complete the square when you can just use the Quadratic Formula to solve a Quadratic Equation?
Well, one reason is given above, where the new form not only shows you the vertex, but makes it easier to solve.
There are also times when the form ax2 + bx + c may be part of a larger problem and rearranging it asa(x+d)2 + e makes the solution easier, because x only appears once.
For example "x" may itself be a function (like cos(z)) and rearranging it may open up a path to a better solution.
Also Completing the Square is the first step in the Derivation of the Quadratic Formula
Just think of it as another tool in your mathematics toolbox.


0 comments:
Post a Comment